MyWikiBiz, Author Your Legacy — Monday December 02, 2024
Jump to navigationJump to searchDifferential Logic
ASCII Graphics
o-------------------------------------------------o
| |
| |
| o-------------o o-------------o |
| / \ / \ |
| / o \ |
| / /%\ \ |
| / /%%%\ \ |
| o o%%%%%o o |
| | |%%%%%| | |
| | P |%%%%%| Q | |
| | |%%%%%| | |
| o o%%%%%o o |
| \ \%%%/ / |
| \ \%/ / |
| \ o / |
| \ / \ / |
| o-------------o o-------------o |
| |
| |
o-------------------------------------------------o
| f = p q |
o-------------------------------------------------o
Figure 22-a. Conjunction pq : X -> B
|
o-------------------------------------------------o
| |
| |
| o-------------o o-------------o |
| / \ / \ |
| / P o Q \ |
| / /%\ \ |
| / /%%%\ \ |
| o o.->-.o o |
| | p(q)(dp)dq |%\%/%| (p)q dp(dq) | |
| | o---------------|->o<-|---------------o | |
| | |%%^%%| | |
| o o%%|%%o o |
| \ \%|%/ / |
| \ \|/ / |
| \ o / |
| \ /|\ / |
| o-------------o | o-------------o |
| | |
| | |
| | |
| o |
| (p)(q) dp dq |
| |
o-------------------------------------------------o
| f = p q |
o-------------------------------------------------o
| |
| Ef = p q (dp)(dq) |
| |
| + p (q) (dp) dq |
| |
| + (p) q dp (dq) |
| |
| + (p)(q) dp dq |
| |
o-------------------------------------------------o
Figure 22-b. Enlargement E[pq] : EX -> B
|
o-------------------------------------------------o
| |
| |
| o-------------o o-------------o |
| / \ / \ |
| / P o Q \ |
| / /%\ \ |
| / /%%%\ \ |
| o o%%%%%o o |
| | (dp)dq |%%%%%| dp(dq) | |
| | o<--------------|->o<-|-------------->o | |
| | |%%^%%| | |
| o o%%|%%o o |
| \ \%|%/ / |
| \ \|/ / |
| \ o / |
| \ /|\ / |
| o-------------o | o-------------o |
| | |
| | |
| v |
| o |
| dp dq |
| |
o-------------------------------------------------o
| f = p q |
o-------------------------------------------------o
| |
| Df = p q ((dp)(dq)) |
| |
| + p (q) (dp) dq |
| |
| + (p) q dp (dq) |
| |
| + (p)(q) dp dq |
| |
o-------------------------------------------------o
Figure 22-c. Difference D[pq] : EX -> B
|
JPEG Graphics
|
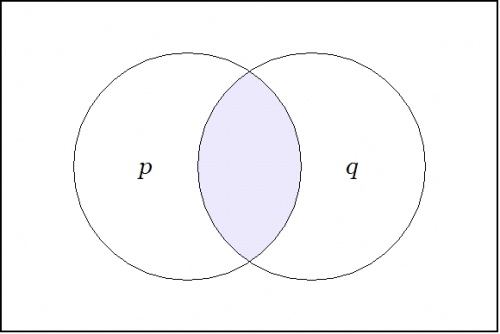
| \(\text{Figure 22-a. Conjunction}~ pq : X \to \mathbb{B}\)
|
|
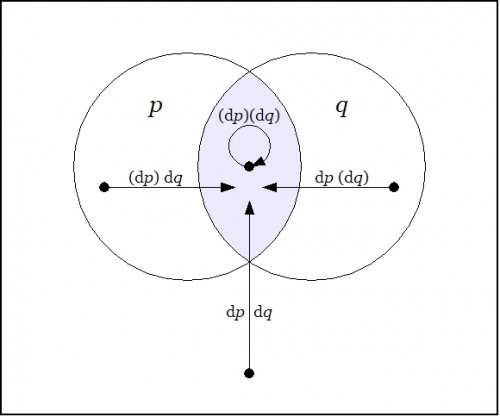
| \(\text{Figure 22-b. Enlargement}~ \operatorname{E}(pq) : \operatorname{E}X \to \mathbb{B}\)
|
|
\(\begin{array}{rcccccc}
\operatorname{E}(pq)
& = & p & \cdot & q & \cdot & (\operatorname{d}p)(\operatorname{d}q)
\\[4pt]
& + & p & \cdot & (q) & \cdot & (\operatorname{d}p)~\operatorname{d}q~
\\[4pt]
& + & (p) & \cdot & q & \cdot & ~\operatorname{d}p~(\operatorname{d}q)
\\[4pt]
& + & (p) & \cdot & (q) & \cdot & ~\operatorname{d}p~~\operatorname{d}q~\end{array}\)
|
|
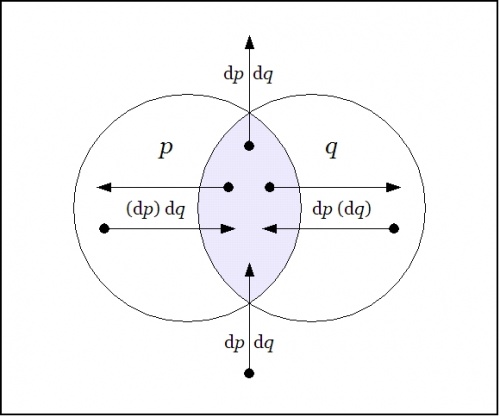
| \(\text{Figure 22-c. Difference}~ \operatorname{D}(pq) : \operatorname{E}X \to \mathbb{B}\)
|
|
\(\begin{array}{rcccccc}
\operatorname{D}(pq)
& = & p & \cdot & q & \cdot & ((\operatorname{d}p)(\operatorname{d}q))
\\[4pt]
& + & p & \cdot & (q) & \cdot & ~(\operatorname{d}p)~\operatorname{d}q~~
\\[4pt]
& + & (p) & \cdot & q & \cdot & ~~\operatorname{d}p~(\operatorname{d}q)~
\\[4pt]
& + & (p) & \cdot & (q) & \cdot & ~~\operatorname{d}p~~\operatorname{d}q~~
\end{array}\)
|
