Difference between revisions of "Directory talk:Jon Awbrey/Papers/Propositional Equation Reasoning Systems"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==Place for Discussion== |
| − | + | … | |
| − | + | ==Formal extension : Cactus calculus (Work Area)== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let us now extend the CSP–GSB calculus in the following way: | |
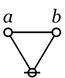
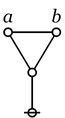
| − | + | The first extension is the ''reflective extension of logical graphs'', or what may be described as the ''cactus language'', after its principal graph-theoretic data structure. It is generated by generalizing the negation operator <math>\texttt{(\_)}</math> in a particular manner, treating <math>\texttt{(\_)}</math> as the ''[[minimal negation operator]]'' of order 1, and adding another such operator for each integer parameter greater than 1. Taken in series, the minimal negation operators are symbolized by parenthesized argument lists of the following shapes: <math>\texttt{(\_)},</math> <math>\texttt{(\_, \_)},</math> <math>\texttt{(\_, \_, \_)},</math> and so on, where the number of argument slots is the order of the reflective negation operator in question. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Cactus Language for Propositional Logic=== |
| − | + | The development of differential logic is greatly facilitated by having a conceptually efficient calculus in place at the level of [[boolean-valued functions]] and elementary logical propositions. A calculus that is very efficient from both conceptual and computational standpoints is based on just two types of logical connectives, both of variable <math>k\!</math>-ary scope. The formulas of this calculus map into a species of graph-theoretical structures called ''painted and rooted cacti'' (PARCs) that lend visual representation to their functional structure and smooth the path to efficient computation. | |
| − | === | + | {| align="center" cellpadding="6" width="90%" |
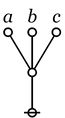
| + | | The first kind of propositional expression is a parenthesized sequence of propositional expressions, written as <math>\texttt{(} e_1 \texttt{,} e_2 \texttt{,} \ldots \texttt{,} e_{k-1} \texttt{,} e_k \texttt{)}</math> and read to say that exactly one of the propositions <math>e_1, e_2, \ldots, e_{k-1}, e_k</math> is false, in other words, that their [[minimal negation]] is true. A clause of this form maps into a PARC structure called a ''lobe'', in this case, one that is ''painted'' with the colors <math>e_1, e_2, \ldots, e_{k-1}, e_k</math> as shown below. | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Cactus Graph Lobe Connective.jpg|500px]] | |
| + | |} | ||
| − | === | + | {| align="center" cellpadding="6" width="90%" |
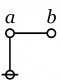
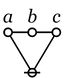
| + | | The second kind of propositional expression is a concatenated sequence of propositional expressions, written as <math>e_1\ e_2\ \ldots\ e_{k-1}\ e_k</math> and read to say that all of the propositions <math>e_1, e_2, \ldots, e_{k-1}, e_k</math> are true, in other words, that their [[logical conjunction]] is true. A clause of this form maps into a PARC structure called a ''node'', in this case, one that is ''painted'' with the colors <math>e_1, e_2, \ldots, e_{k-1}, e_k</math> as shown below. | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Cactus Graph Node Connective.jpg|500px]] | ||
| + | |} | ||
| − | < | + | All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the parenthesized form is sufficient to define the concatenated form, making the latter formally dispensable, but it is convenient to maintain it as a concise way of expressing more complicated combinations of parenthesized forms. While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives. In contexts where ordinary parentheses are needed for other purposes an alternate typeface <math>\texttt{(} \ldots \texttt{)}</math> may be used for logical operators. |
| − | |||
| − | + | Table 1 collects a sample of basic propositional forms as expressed in terms of cactus language connectives. | |
| − | + | <br> | |
| − | + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | |
| + | |+ <math>\text{Table 1.}~~\text{Syntax and Semantics of a Calculus for Propositional Logic}</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | <math>\text{Graph}\!</math> | ||
| + | | <math>\text{Expression}\!</math> | ||
| + | | <math>\text{Interpretation}\!</math> | ||
| + | | <math>\text{Other Notations}\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Rooted Node.jpg|20px]] | ||
| + | | <math>~</math> | ||
| + | | <math>\operatorname{true}</math> | ||
| + | | <math>1\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Rooted Edge.jpg|20px]] | ||
| + | | <math>\texttt{(~)}</math> | ||
| + | | <math>\operatorname{false}</math> | ||
| + | | <math>0\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Cactus A Big.jpg|20px]] | ||
| + | | <math>a\!</math> | ||
| + | | <math>a\!</math> | ||
| + | | <math>a\!</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A) Big.jpg|20px]] | ||
| + | | <math>\texttt{(} a \texttt{)}</math> | ||
| + | | <math>\operatorname{not}~ a</math> | ||
| + | | <math>\lnot a \quad \bar{a} \quad \tilde{a} \quad a^\prime</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Cactus ABC Big.jpg|50px]] | ||
| + | | <math>a ~ b ~ c</math> | ||
| + | | <math>a ~\operatorname{and}~ b ~\operatorname{and}~ c</math> | ||
| + | | <math>a \land b \land c</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus ((A)(B)(C)) Big.jpg|65px]] | ||
| + | | <math>\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}</math> | ||
| + | | <math>a ~\operatorname{or}~ b ~\operatorname{or}~ c</math> | ||
| + | | <math>a \lor b \lor c</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A(B)) Big.jpg|60px]] | ||
| + | | <math>\texttt{(} a \texttt{(} b \texttt{))}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a ~\operatorname{implies}~ b | ||
| + | \\[6pt] | ||
| + | \operatorname{if}~ a ~\operatorname{then}~ b | ||
| + | \end{matrix}</math> | ||
| + | | <math>a \Rightarrow b</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A,B) Big.jpg|65px]] | ||
| + | | <math>\texttt{(} a \texttt{,} b \texttt{)}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a ~\operatorname{not~equal~to}~ b | ||
| + | \\[6pt] | ||
| + | a ~\operatorname{exclusive~or}~ b | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a \neq b | ||
| + | \\[6pt] | ||
| + | a + b | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus ((A,B)) Big.jpg|65px]] | ||
| + | | <math>\texttt{((} a \texttt{,} b \texttt{))}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a ~\operatorname{is~equal~to}~ b | ||
| + | \\[6pt] | ||
| + | a ~\operatorname{if~and~only~if}~ b | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a = b | ||
| + | \\[6pt] | ||
| + | a \Leftrightarrow b | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A,B,C) Big.jpg|65px]] | ||
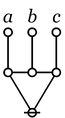
| + | | <math>\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \operatorname{just~one~of} | ||
| + | \\ | ||
| + | a, b, c | ||
| + | \\ | ||
| + | \operatorname{is~false}. | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | & \bar{a} ~ b ~ c | ||
| + | \\ | ||
| + | \lor & a ~ \bar{b} ~ c | ||
| + | \\ | ||
| + | \lor & a ~ b ~ \bar{c} | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus ((A),(B),(C)) Big.jpg|65px]] | ||
| + | | <math>\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \operatorname{just~one~of} | ||
| + | \\ | ||
| + | a, b, c | ||
| + | \\ | ||
| + | \operatorname{is~true}. | ||
| + | \\[6pt] | ||
| + | \operatorname{partition~all} | ||
| + | \\ | ||
| + | \operatorname{into}~ a, b, c. | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | & a ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ b ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ \bar{b} ~ c | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
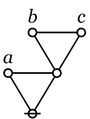
| + | | height="160px" | [[Image:Cactus (A,(B,C)) Big.jpg|90px]] | ||
| + | | <math>\texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \operatorname{oddly~many~of} | ||
| + | \\ | ||
| + | a, b, c | ||
| + | \\ | ||
| + | \operatorname{are~true}. | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <p><math>a + b + c\!</math></p> | ||
| + | <br> | ||
| + | <p><math>\begin{matrix} | ||
| + | & a ~ b ~ c | ||
| + | \\ | ||
| + | \lor & a ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ b ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ \bar{b} ~ c | ||
| + | \end{matrix}</math></p> | ||
| + | |- | ||
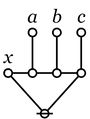
| + | | height="160px" | [[Image:Cactus (X,(A),(B),(C)) Big.jpg|90px]] | ||
| + | | <math>\texttt{(} x \texttt{,(} a \texttt{),(} b \texttt{),(} c \texttt{))}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \operatorname{partition}~ x | ||
| + | \\ | ||
| + | \operatorname{into}~ a, b, c. | ||
| + | \\[6pt] | ||
| + | \operatorname{genus}~ x ~\operatorname{comprises} | ||
| + | \\ | ||
| + | \operatorname{species}~ a, b, c. | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | & \bar{x} ~ \bar{a} ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & x ~ a ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & x ~ \bar{a} ~ b ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & x ~ \bar{a} ~ \bar{b} ~ c | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | + | The simplest expression for logical truth is the empty word, usually denoted by <math>\varepsilon\!</math> or <math>\lambda\!</math> in formal languages, where it forms the identity element for concatenation. To make it visible in context, it may be denoted by the equivalent expression <math>{}^{\backprime\backprime} \texttt{((~))} {}^{\prime\prime},</math> or, especially if operating in an algebraic context, by a simple <math>{}^{\backprime\backprime} 1 {}^{\prime\prime}.</math> Also when working in an algebraic mode, the plus sign <math>{}^{\backprime\backprime} + {}^{\prime\prime}</math> may be used for [[exclusive disjunction]]. For example, we have the following paraphrases of algebraic expressions by means of parenthesized expressions: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="6" style="text-align:center" | |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a + b | ||
| + | & = & | ||
| + | \texttt{(} a \texttt{,} b \texttt{)} | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a + b + c | ||
| + | & = & | ||
| + | \texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))} | ||
| + | & = & | ||
| + | \texttt{((} a \texttt{,} b \texttt{),} c \texttt{)} | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | + | It is important to note that the last expressions are not equivalent to the 3-place parenthesis <math>\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}.</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
Latest revision as of 03:28, 1 October 2010
Place for Discussion
…
Formal extension : Cactus calculus (Work Area)
Let us now extend the CSP–GSB calculus in the following way:
The first extension is the reflective extension of logical graphs, or what may be described as the cactus language, after its principal graph-theoretic data structure. It is generated by generalizing the negation operator \(\texttt{(\_)}\) in a particular manner, treating \(\texttt{(\_)}\) as the minimal negation operator of order 1, and adding another such operator for each integer parameter greater than 1. Taken in series, the minimal negation operators are symbolized by parenthesized argument lists of the following shapes\[\texttt{(\_)},\] \(\texttt{(\_, \_)},\) \(\texttt{(\_, \_, \_)},\) and so on, where the number of argument slots is the order of the reflective negation operator in question.
Cactus Language for Propositional Logic
The development of differential logic is greatly facilitated by having a conceptually efficient calculus in place at the level of boolean-valued functions and elementary logical propositions. A calculus that is very efficient from both conceptual and computational standpoints is based on just two types of logical connectives, both of variable \(k\!\)-ary scope. The formulas of this calculus map into a species of graph-theoretical structures called painted and rooted cacti (PARCs) that lend visual representation to their functional structure and smooth the path to efficient computation.
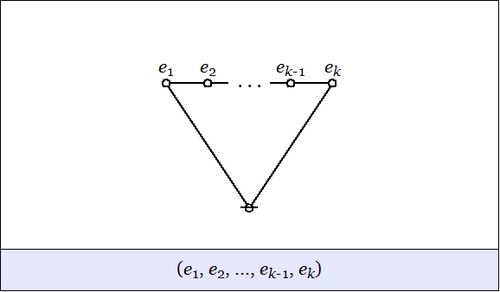
| The first kind of propositional expression is a parenthesized sequence of propositional expressions, written as \(\texttt{(} e_1 \texttt{,} e_2 \texttt{,} \ldots \texttt{,} e_{k-1} \texttt{,} e_k \texttt{)}\) and read to say that exactly one of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\) is false, in other words, that their minimal negation is true. A clause of this form maps into a PARC structure called a lobe, in this case, one that is painted with the colors \(e_1, e_2, \ldots, e_{k-1}, e_k\) as shown below. |
|
| The second kind of propositional expression is a concatenated sequence of propositional expressions, written as \(e_1\ e_2\ \ldots\ e_{k-1}\ e_k\) and read to say that all of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\) are true, in other words, that their logical conjunction is true. A clause of this form maps into a PARC structure called a node, in this case, one that is painted with the colors \(e_1, e_2, \ldots, e_{k-1}, e_k\) as shown below. |

|
All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the parenthesized form is sufficient to define the concatenated form, making the latter formally dispensable, but it is convenient to maintain it as a concise way of expressing more complicated combinations of parenthesized forms. While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives. In contexts where ordinary parentheses are needed for other purposes an alternate typeface \(\texttt{(} \ldots \texttt{)}\) may be used for logical operators.
Table 1 collects a sample of basic propositional forms as expressed in terms of cactus language connectives.
The simplest expression for logical truth is the empty word, usually denoted by \(\varepsilon\!\) or \(\lambda\!\) in formal languages, where it forms the identity element for concatenation. To make it visible in context, it may be denoted by the equivalent expression \({}^{\backprime\backprime} \texttt{((~))} {}^{\prime\prime},\) or, especially if operating in an algebraic context, by a simple \({}^{\backprime\backprime} 1 {}^{\prime\prime}.\) Also when working in an algebraic mode, the plus sign \({}^{\backprime\backprime} + {}^{\prime\prime}\) may be used for exclusive disjunction. For example, we have the following paraphrases of algebraic expressions by means of parenthesized expressions:
|
\(\begin{matrix} a + b & = & \texttt{(} a \texttt{,} b \texttt{)} \end{matrix}\) |
|
\(\begin{matrix} a + b + c & = & \texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))} & = & \texttt{((} a \texttt{,} b \texttt{),} c \texttt{)} \end{matrix}\) |
It is important to note that the last expressions are not equivalent to the 3-place parenthesis \(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}.\)